グラフデータと経路

1. グラフデータと経路#

Hide code cell source 
import numpy as np
import networkx as nx

%matplotlib inline
Hide code cell source 
DRAW_CONFIG = {
    'node_color': 'white',
    'edgecolors': 'black', # line color of nodes
    'with_labels': True,
    'node_size': 600,
    'font_size': 14,
    'font_family': 'Arial',
}

1.1. グラフとは#

グラフ（graph） とは，以下の図のように「点」と「つながり」によって表されるデータである． 事物間の関係性を抽象化することができる強力なデータ構造である． 分野によっては，グラフのことをネットワークと呼ぶこともある．

数学的には，グラフはノード（node） の集合とエッジ（edge） の集合から構成されるデータを意味する． ノードはグラフを構成する要素であり，頂点と呼ばれることもある． エッジはノード間の連結関係を示すものであり，枝と呼ばれることもある． エッジは重みを持つことがある．

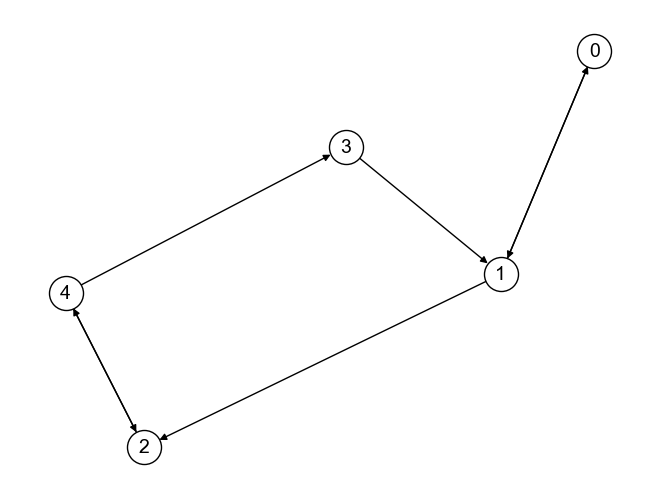
../_images/bb47be3210a1591d699e73e53c507d9b24c6ab6fc83407634b700ce675c2c70a.png

グラフには，

  • エッジに方向性を有する有向グラフ（directed graph）

  • エッジに方向性を有しない無向グラフ（undirected graph）

の2種類に大別される．

以下は有向グラフの例．

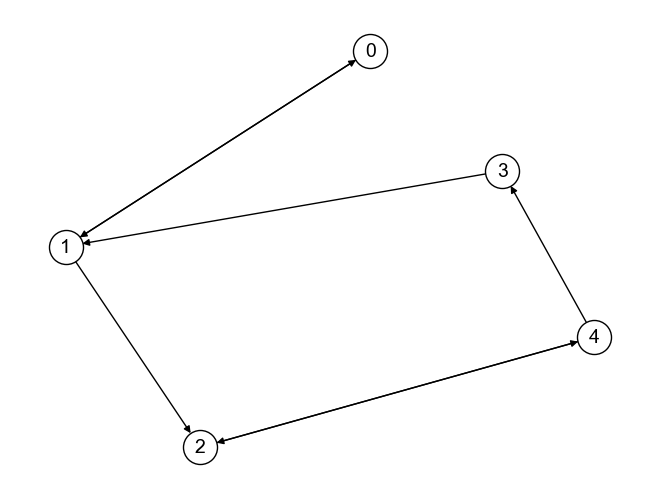
../_images/2017e9b0dea0962dc68c6f426f1c1922bf175b257d5aa8acfa852d6dc1641887.png

以下は，上記有向グラフのエッジから方向性を除いた無向グラフ．

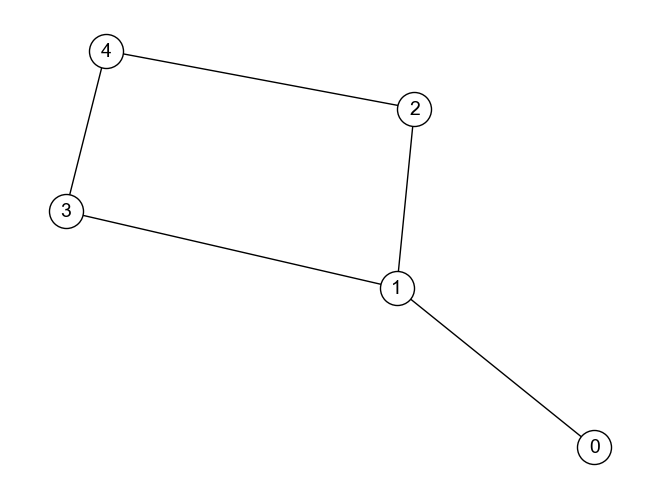
../_images/c3adaf2f3ef36a8611f7fe33eb3b73cfc75687901e6d6010aacad20313e9e4b7.png

1.1.1. NetworkXでグラフを定義する#

NetworkXは，グラフを効率的に扱うためのPythonライブラリである． NetworkXを使うには，以下のようにライブラリをインポートする．

import networkx as nx
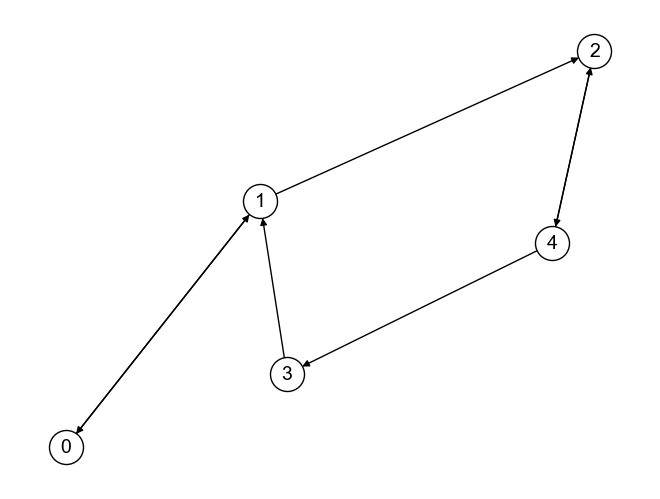
../_images/4cfa00394e66a0f5ff5bef6c9e92eeeb6ee3e5248e2eb2400fc84d17fc0b6444.png

さて，上のグラフをNetworkXで定義してみよう． 以下のコードを実行すると，上の有向グラフを定義し可視化できる．

# ノードの集合
V = [0, 1, 2, 3, 4]

# エッジの集合
E = [(0, 1), (1, 0), (1, 2),
     (2, 4), (3, 1), (4, 2),
     (4, 3)]

G = nx.DiGraph() # 空の有効グラフを用意
G.add_nodes_from(V) # ノードの追加
G.add_edges_from(E) # エッジの追加

# グラフGの可視化
nx.draw(G, with_labels=True)
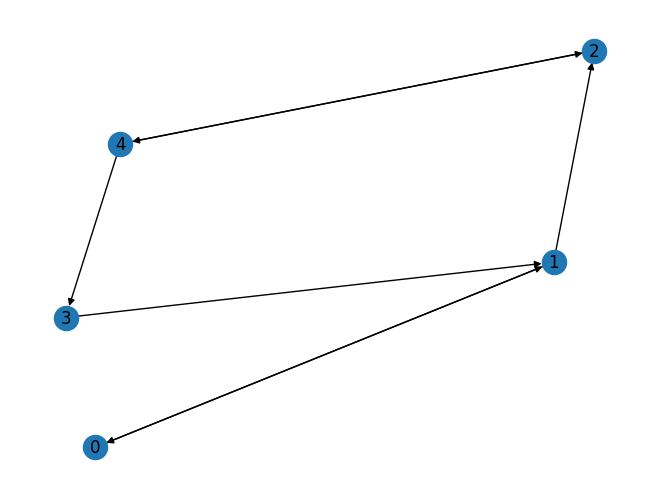
../_images/9c8a9239fed6ef364634fb961300ef81a26ec7b7643764d516ff6937650a44d7.png

次は上記グラフを無向グラフ化したものを定義してみよう． 以下がそのコードである．

# ノードの集合
V = [0, 1, 2, 3, 4]

# エッジの集合
E = [(0, 1), (1, 2),
     (1, 0), # これを書いても(0, 1)があるので無視される
     (2, 4), (3, 1),
     (4, 2), # これを書いても(2, 4)があるので無視される
     (4, 3)
]

G_undirected = nx.Graph() # 空の無効グラフを用意（DiGraphではない事に注意）
G_undirected.add_nodes_from(V) # ノードの追加
G_undirected.add_edges_from(E) # エッジの追加

# グラフGの可視化
nx.draw(G_undirected, with_labels=True)
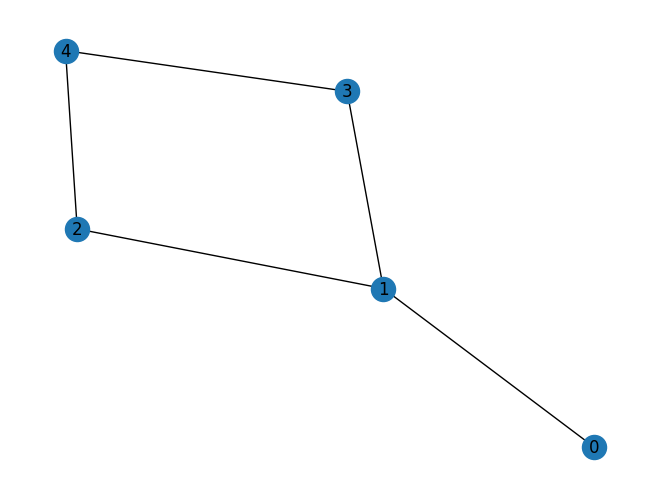
../_images/9873a16b5d9a1e07f1fd0f2b72fcf2319c83102e8d35f685fe439d02a20b3079.png

定義したグラフのノードとエッジを確認してみよう． 以下のコードでグラフのノード集合とエッジ集合を取得することができる．

# ノードの取得
V = G_undirected.nodes()

# エッジの取得
E = G_undirected.edges()

# エッジを表示してみる
for edge in E:
    print(edge)

(0, 1)
(1, 2)
(1, 3)
(2, 4)
(3, 4)

1.1.2. 隣接行列#

グラフにおけるノードの接続関係を示す行列は隣接行列（adjacency matrix） と呼ばれる． 以下のグラフ\(G\)の隣接行列を考えてみよう．

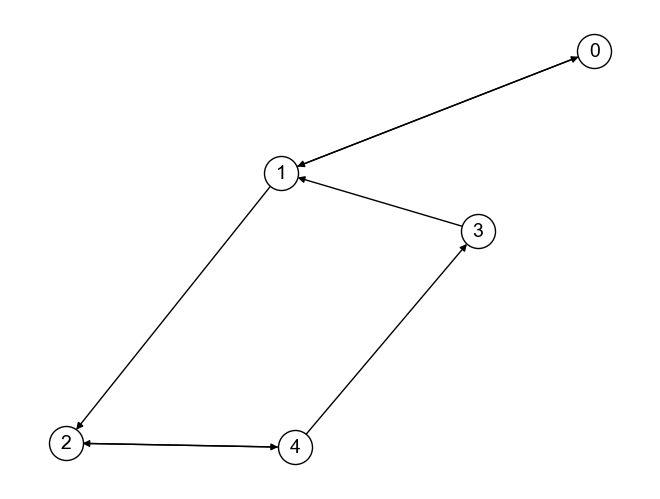
../_images/8478c2bc669edc082d68a8b43e0ca4dcb11408367b427fb725d38c2919871235.png

上記グラフ\(G\)の隣接行列\(A\)は，

\[\begin{split} \boldsymbol{A} = \left[\begin{array}{ccccc} 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \\ \end{array}\right] \end{split}\]

となる．

NetworkXでグラフ\(G\)の隣接行列\(A\)（numpy.ndarray形式）を取得するには，以下のようにする．

A = nx.adjacency_matrix(G).toarray()

A

array([[0, 1, 0, 0, 0],
       [1, 0, 1, 0, 0],
       [0, 0, 0, 0, 1],
       [0, 1, 0, 0, 0],
       [0, 0, 1, 1, 0]])

ちなみに，NetworkXでグラフに属する任意のノードの隣接ノードを取得するにはneighborsメソッドを使う． 以下は，グラフ\(G\)に属するノード1の隣接ノードを取得するコードである．

neighbors = list(G.neighbors(1))

neighbors

[0, 2]

1.2. 経路#

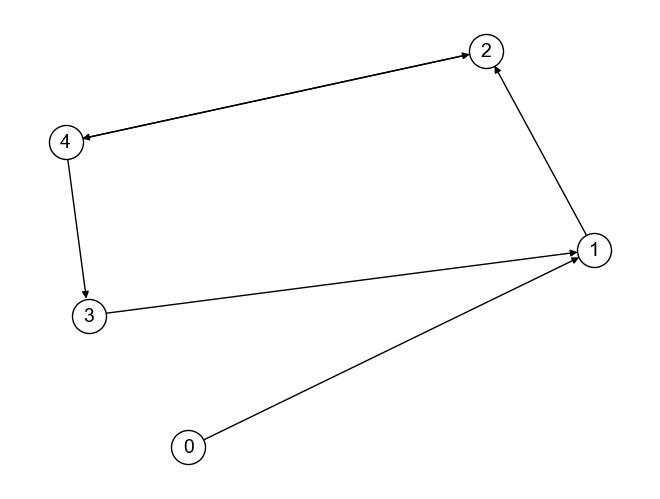
../_images/82b206a90a3ba5dd1b061247d1b2b6b1b0aec327e9ee40f3f84c0558a417c364.png

グラフ上のエッジをたどって，あるノードから別ノードに移動する際に通るノードの系列を経路（path） と呼ぶ． 例えば，上記グラフにおいてノード4からノード2に至る経路は\((4, 2), (4, 3, 1, 2)\)などがある．

1.2.1. 到達可能性#

ノード\(n_x\)からノード\(n_y\)への経路が存在するとき，\(n_x\)から\(n_y\)へ到達可能という． 例えば，上記グラフにおいて，ノード0からノード3へは到達可能である． 一方，ノード3からノード0へは到達不可能である．

重みなし行列の場合，隣接行列のべき乗を計算することで到達可能性を調べられる． グラフ\(G\)の隣接行列を\(A\)としたとき，\(A^k\)のm行n列目の値は，m番目のノードからn番目のノードへkホップで到達できる経路がいくつあるかを示す．

例えば，上記グラフ\(G\)の隣接行列\(A\)は

\[\begin{split} \boldsymbol{A} = \left[\begin{array}{ccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \\ \end{array}\right] \end{split}\]

であるが，\(A^2\)は

\[\begin{split} \boldsymbol{A^2} = \left[\begin{array}{ccccc} 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 \\ \end{array}\right] \end{split}\]

となる． \(A^2\)において0行2列目の値は1であるが，これは「ノード0からノード2まで2ホップで到達できるノードは1つある」ことを意味している（その経路は\((0, 1, 2)\)）．

隣接行列のべき乗を計算すれば，任意のノードからノードへnホップで到達可能かどうかを調べることができる． これはNetworkXでも簡単にできる． 以下は，上記グラフ\(G\)の到達可能性を調べるコード例である．

# 隣接行列の取得
A = nx.adjacency_matrix(G).toarray()

# Aの2乗を計算
A @ A

array([[0, 0, 1, 0, 0],
       [0, 0, 0, 0, 1],
       [0, 0, 1, 1, 0],
       [0, 0, 1, 0, 0],
       [0, 1, 0, 0, 1]])

# Aのn乗の第(i, j)成分の値は，グラフGのノードiからノードjまでnホップで到達できる経路がいくつあるかを示す
np.linalg.matrix_power(A, 3)

array([[0, 0, 0, 0, 1],
       [0, 0, 1, 1, 0],
       [0, 1, 0, 0, 1],
       [0, 0, 0, 0, 1],
       [0, 0, 2, 1, 0]])

1.2.2. 距離#

ノード\(n_x\)からノード\(n_y\)への最短経路の長さを距離（distance） と呼ぶ． グラフのエッジに重みがある場合，距離は最短経路上のエッジの重みの合計値となる．

../_images/82b206a90a3ba5dd1b061247d1b2b6b1b0aec327e9ee40f3f84c0558a417c364.png

例えば，上記グラフ\(G\)において，ノード4からノード2への最短経路は\((4, 2)\)である． よって，ノード4からノード2への距離は1である．

NetworkXを用いて指定したノード間の最短経路を取得するには，shortest_path関数を用いる． 以下は，上記グラフ\(G\)に属するノード0からノード4への最短経路を取得するコードである．

# sourceは始点，targetは終点
shortest_path = nx.shortest_path(G, source=0, target=4)
shortest_path

[0, 1, 2, 4]

あるノードから他のノードへの最短経路を取得するには，single_source_all_shortest_paths関数を用いる． 以下は，上記グラフ\(G\)に属するノード3から到達できるすべてのノードとそこまでの最短経路を取得するコードである．

# 返り値は dict[node, shortestpath] 形式の辞書（ジェネレータ）
shortest_paths = dict(nx.single_source_all_shortest_paths(G, 3))

# 表示
for node_to, shortest_path in shortest_paths.items():
    print(f'ノード{node_to}への最短経路: {shortest_path}')

ノード1への最短経路: [[3, 1]]
ノード2への最短経路: [[3, 1, 2]]
ノード3への最短経路: [[3]]
ノード4への最短経路: [[3, 1, 2, 4]]

NetworkXを用いて，グラフ上の全ノード間の最短経路を取得するには，all_pairs_shortest_pathメソッドを用いる． 以下は，上記グラフ\(G\)に属する全ノード間の最短経路を取得するコードである．

# 返り値は dict[node, shortestpath] 形式の辞書（ジェネレータ）
shortest_paths = dict(nx.all_pairs_shortest_path(G))

# 表示
for node_from, shortest_paths in shortest_paths.items():
    for node_to, shortest_path in shortest_paths.items():
        print(f'ノード{node_from}からノード{node_to}への最短経路: {shortest_path}')

ノード0からノード0への最短経路: [0]
ノード0からノード1への最短経路: [0, 1]
ノード0からノード2への最短経路: [0, 1, 2]
ノード0からノード4への最短経路: [0, 1, 2, 4]
ノード0からノード3への最短経路: [0, 1, 2, 4, 3]
ノード1からノード1への最短経路: [1]
ノード1からノード2への最短経路: [1, 2]
ノード1からノード4への最短経路: [1, 2, 4]
ノード1からノード3への最短経路: [1, 2, 4, 3]
ノード2からノード2への最短経路: [2]
ノード2からノード4への最短経路: [2, 4]
ノード2からノード3への最短経路: [2, 4, 3]
ノード2からノード1への最短経路: [2, 4, 3, 1]
ノード3からノード3への最短経路: [3]
ノード3からノード1への最短経路: [3, 1]
ノード3からノード2への最短経路: [3, 1, 2]
ノード3からノード4への最短経路: [3, 1, 2, 4]
ノード4からノード4への最短経路: [4]
ノード4からノード2への最短経路: [4, 2]
ノード4からノード3への最短経路: [4, 3]
ノード4からノード1への最短経路: [4, 3, 1]

グラフに属する全ノード間の距離を表記した行列を距離行列（distance matrix） と呼ぶ． 上記グラフ\(G\)の距離行列\(D\)は

\[\begin{split} \boldsymbol{D} = \left[\begin{array}{ccccc} 0 & 1 & 2 & 4 & 4 \\ \infty & 0 & 1 & 3 & 2 \\ \infty & 3 & 0 & 2 & 1 \\ \infty & 1 & 2 & 0 & 3 \\ \infty & 2 & 1 & 1 & 0 \\ \end{array}\right] \end{split}\]

となる．

NetworkXを用いて，グラフの距離行列を取得するにはfloyd_warshall_numpyメソッドを用いる． このメソッドを用いると，距離行列がnumpy.ndarray形式で得られる．

以下は上図のグラフ\(G\)の距離行列を取得するコードである．

# ワーシャルフロイド法による距離行列の算出
nx.floyd_warshall_numpy(G)

array([[ 0.,  1.,  2.,  4.,  3.],
       [inf,  0.,  1.,  3.,  2.],
       [inf,  3.,  0.,  2.,  1.],
       [inf,  1.,  2.,  0.,  3.],
       [inf,  2.,  1.,  1.,  0.]])

1.3. クイズ#

1.3.1. Q1: グラフの定義#

NetworkXを使って以下のグラフを定義し，可視化しなさい．

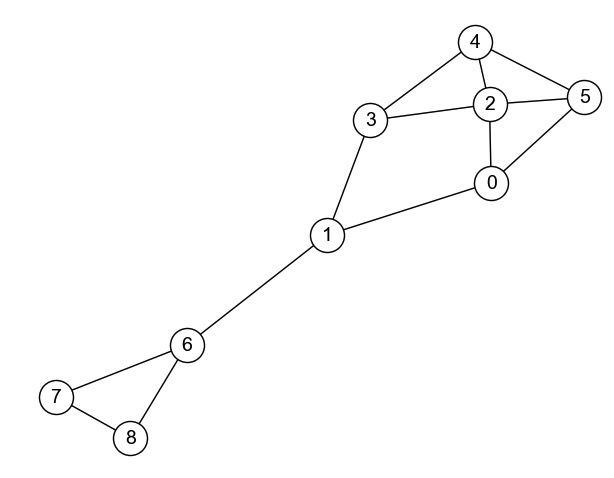
1.3.2. Q2: 到達可能性#

Q1で定義したグラフについて，ノード4からノード6に4ホップで到達できる経路はいくつあるかを求めなさい．

1.3.3. Q3: ソーシャルグラフ#

SNAP Facebook Datasetは，スタンフォード大学のソーシャルネットワーク分析プロジェクトが公開しているデータセットの一つである． このデータセットにはFacebookから抽出したユーザ間のつながり（フレンド関係）が格納されている．

以下のコードは，データセットを読み込み，NetworkXのグラフ形式に変換し，グラフを可視化するコードである． 読み込んだグラフ（G_facebook）に対して最短経路アルゴリズムを適用し，グラフ上の全ノード間の距離を計算しなさい． その上で，計算したノード間の距離の平均値を求めなさい．

import pandas as pd
import networkx as nx

# データのダウンロード via pandas
facebook_df = pd.read_csv(
    "https://snap.stanford.edu/data/facebook_combined.txt.gz",
    compression="gzip",
    sep=" ",
    names=["start_node", "end_node"],
)

# NetworkXのグラフに変換
G_facebook = nx.from_pandas_edgelist(facebook_df, "start_node", "end_node")

# 表示位置を調整して可視化
pos = nx.spring_layout(G_facebook, iterations=15, seed=1721)
nx.draw(G_facebook, pos, node_size=10, with_labels=False, width=0.15, alpha=0.5)
../_images/d99fe178faee286041e7659ebd47f3ad03e77c1db875bf27024229d2ccba775c.png
Contents