ウェブとグラフ#
Show code cell source
import numpy as np
import networkx as nx
%matplotlib inline
クイズ#
Q1: デッドリンク,スパイダートラップのあるグラフ#
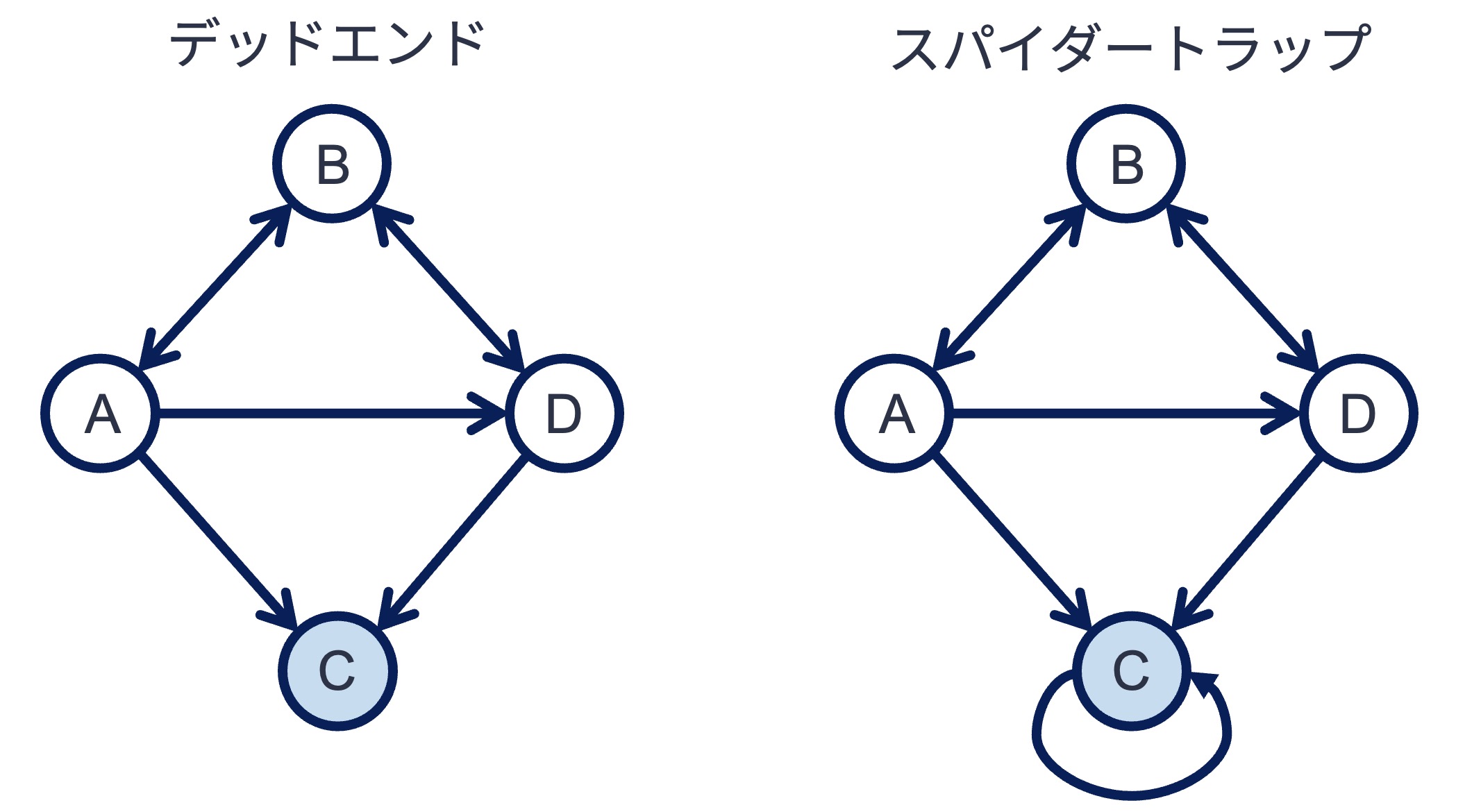
上記の各グラフに対してシンプルなPageRankアルゴリズムを適用すると,どのような値に収束するか. Pythonコードを書いて確かめなさい.
import networkx as nx
# グラフの定義
G_deadend = nx.DiGraph([
('A', 'B'), ('A', 'C'), ('A', 'D'),
('B', 'A'), ('B', 'D'),
('D', 'B'),
])
G_spidertrap = nx.DiGraph([
('A', 'B'), ('A', 'C'), ('A', 'D'),
('B', 'A'), ('B', 'D'),
('C', 'C'), ('D', 'B'),
])
# Write your codes below
import networkx as nx
import numpy as np
# 行列の正規化のために使う
from sklearn.preprocessing import normalize
def calc_simple_pagerank(G, iter_count=100):
# PageRankベクトルを初期化する
N = G.number_of_nodes()
p = np.ones(N).reshape(-1, 1) # 要素値1,要素数がNの縦ベクトル
p = p / N
# 隣接行列
A = nx.adjacency_matrix(G).toarray()
# 遷移確率行列
M = normalize(A, norm='l1', axis=1)
# PageRank値の更新.100回も繰り返せば値は収束する
for i in range(iter_count):
p = np.dot(M.T, p)
return p
# グラフの定義
G_deadend = nx.DiGraph([
('A', 'B'), ('A', 'C'), ('A', 'D'),
('B', 'A'), ('B', 'D'),
('D', 'B'),
])
G_spidertrap = nx.DiGraph([
('A', 'B'), ('A', 'C'), ('A', 'D'),
('B', 'A'), ('B', 'D'),
('C', 'C'), ('D', 'B'),
])
calc_simple_pagerank(G_deadend, iter_count=1000)
array([[2.28742507e-37],
[4.21206421e-37],
[8.28147147e-38],
[3.11557222e-37]])
calc_simple_pagerank(G_spidertrap, iter_count=1000)
array([[2.28742507e-37],
[4.21206421e-37],
[1.00000000e+00],
[3.11557222e-37]])
Q2: PageRank実装#
NetworkXのpagerank関数を用いずに,(完全な)PageRank値を計算する関数calc_pagerankを実装しなさい.
なお,calc_pagerank関数の引数は以下としなさい:
第1引数: NetworkX形式のグラフ\(G\)
第2引数: \(\alpha\)パラメータ.デフォルト値は0.85
第3引数: 更新回数.デフォルト値は50
import networkx as nx
import numpy as np
from sklearn.preprocessing import normalize
def calc_pagerank(G, alpha=0.85, iteration_num=50):
n = G.number_of_nodes()
# 隣接行列
A = nx.adjacency_matrix(G).toarray()
# 遷移確率行列
M = normalize(A, norm='l1', axis=1)
# PageRankベクトル
p = np.ones(n).reshape(-1, 1)
p = normalize(p, norm='l1', axis=0)
# Random jumpベクトル
e = np.ones(n).reshape(-1, 1)
for step in range(iteration_num):
p = alpha * np.dot(M.T, p) + (1-alpha) * (e / n)
# スコアとノードを紐付ける
# pはPageRankの縦ベクトルで,スコアはG.nodes()のリスト順に並んでいる
nodes = G.nodes()
scores = {}
for node, score in zip(nodes, p):
scores[node] = score[0]
return scores
calc_pagerank(G_deadend, alpha=0.85, iteration_num=100)
# networkxのpagerank関数で計算
# nx.pagerank(G_deadend, alpha=0.85)
{'A': np.float64(0.1284619622389122),
'B': np.float64(0.2140281464438752),
'C': np.float64(0.07389755596778783),
'D': np.float64(0.1648595182067)}
calc_pagerank(G_spidertrap, alpha=0.85, iteration_num=100)
# networkxのpagerank関数で計算
# nx.pagerank(G_spidertrap, alpha=0.85)
{'A': np.float64(0.1284619622389122),
'B': np.float64(0.2140281464438752),
'C': np.float64(0.4926503731105125),
'D': np.float64(0.1648595182067)}
Q3: 江戸時代の人物#
コチラからダウンロードできるファイル(edo.gml)は,Wikipediaの江戸時代の人物一覧に掲載された歴史上の人物をノード,人物記事から人物記事へのリンクをエッジとするグラフデータを格納したものである.
例えば,江戸時代の人物一覧に掲載されている徳川家康の記事には,同じく江戸時代の人物一覧に掲載された伊達政宗への記事へのリンクが存在するため,グラフ中では徳川家康ノードから伊達政宗ノードへエッジが存在する.
※ 江戸時代に活躍した人物でも江戸時代の人物一覧に掲載されていない人物も存在する.例えば,坂本龍馬は幕末の人物一覧には掲載されているが,江戸時代の人物一覧には掲載されていない.

上のグラフ\(G_{edo}\)は,ダウンロードしたファイルedo.gmlをNetworkXで読み込み,可視化したものである.
グラフ\(G_{edo}\)にPageRankアルゴリズムを適用し,江戸時代の人物のPageRankスコア上位30名を求めなさい.
なお,コチラからダウンロードしたファイルedo.gmlをNetworkXで読み込むには,以下のコードを実行するとよい.
# ダウンロードしたファイルは`../../data/edo.gml`にあるとする(ファイルの保存先はどこでもよい)
G_edo = nx.read_gml("../../data/edo.gml")
sorted(nx.pagerank(G_edo).items(), key=lambda x: -x[1])[:30]
[('徳川家康', 0.018839762302814107),
('徳川秀忠', 0.014647218544087416),
('徳川家光', 0.014047416609427236),
('徳川家斉', 0.012598052079051706),
('本居宣長', 0.011830566523394653),
('徳川吉宗', 0.011773042353908645),
('徳川綱吉', 0.011379371758192062),
('徳川家綱', 0.011171561521555138),
('徳川慶喜', 0.011138666353330481),
('徳川家茂', 0.010507868445224694),
('徳川家慶', 0.009884146816649652),
('松平定信', 0.009392933122066285),
('徳川家宣', 0.008896610471324763),
('徳川家治', 0.008604448734614417),
('徳川家定', 0.008493599171781604),
('明治天皇', 0.007086237830509613),
('徳川家重', 0.007052635452644552),
('後水尾天皇', 0.006904194401312377),
('徳川家継', 0.006611535953116792),
('勝海舟', 0.0064994578679011105),
('孝明天皇', 0.0060884018726106515),
('新井白石', 0.005977341340214977),
('土井利勝', 0.0059182449246124634),
('井伊直弼', 0.005901239051554294),
('水野忠邦', 0.005813149832871907),
('霊元天皇', 0.005774414315342403),
('徳川光圀', 0.005711989954209582),
('徳川斉昭', 0.005482055689677943),
('後陽成天皇', 0.005434813926403158),
('堀田正俊', 0.005354027523454542)]
Q4: Biased PageRank#
オリジナルのPageRankアルゴリズムでは,ページに直接ジャンプする行動に対応する項のベクトルの要素値(以下の式の第2項)は,すべて\(\frac{1}{N}\)としていた. このベクトルを調整することで,特定ノードの影響を強めてPageRankの値を補正することができる.
Q3のPageRankの計算にて,直接ジャンプ項のベクトルの要素値について,
賴山陽,本居宣長,杉田玄白,関孝和に対応する値は\(\frac{1}{4}\)に
上記人物以外についてはゼロ
になるように設定し,再度PageRankを計算し,その値の上位30位の人物を求めなさい.
ヒント: NetworkXのpagerank関数を用いず自力で行列計算で行う場合は,賴山陽,本居宣長,杉田玄白,関孝和の値がベクトルの何番目に対応するかを調べる必要がある.
sorted(nx.pagerank(G_edo, personalization={'頼山陽': 1, '本居宣長': 1, '杉田玄白': 1, '関孝和': 1}).items(), key=lambda x: -x[1])[:30]
[('本居宣長', 0.05294197147616238),
('頼山陽', 0.04865239702615813),
('杉田玄白', 0.04612835279276951),
('関孝和', 0.04044423029554557),
('徳川家康', 0.021165746468947495),
('松平定信', 0.015156447218174232),
('青木木米', 0.014676176541022448),
('徳川家宣', 0.014377544173175227),
('徳川家斉', 0.012966685400068189),
('田能村竹田', 0.012829374427864422),
('徳川吉宗', 0.010273675810803597),
('徳川秀忠', 0.010045276685500728),
('前野良沢', 0.009550512653600216),
('徳川家光', 0.009474795245899703),
('大塩平八郎', 0.00915260213827142),
('徳川忠長', 0.008788925118252702),
('広瀬淡窓', 0.00874965211440414),
('徳川綱吉', 0.008542533098561473),
('賀茂真淵', 0.008375863909818452),
('平賀源内', 0.008148224134917779),
('吉田光由', 0.007691175715584278),
('徳川家綱', 0.0076813868698666216),
('桂川甫周', 0.007643382451930731),
('荻生徂徠', 0.00739579264262577),
('徳川家茂', 0.00715096531559155),
('中川淳庵', 0.007106550328599372),
('上田秋成', 0.0069757039831886206),
('角倉了以', 0.006923711051102907),
('渋川春海', 0.0066795973448305875),
('徳川慶喜', 0.0066363912722926304)]
